Recently I found myself planning a bachelor party. I was aiming to rent a house for 19 friends strewn across the northeastern United States. I wanted to pick a a central location easy for everyone to get to. So, like any normal person (at least one who works in analytics), I wanted to quantitatively determine the most fair location.
“In the Middle”
Very often, when you want to meet someone who lives elsewhere, we pick a point halfway between. This intuitively makes sense when a couple in New York and another in Washington, DC, decides to meet in Philadelphia. This is tidy enough when you have two groups, but what if you have more?
Spatial Mean
Simply put, the Spatial Mean, or Mean Center (described their by Esri) is the same concept (meeting in the middle), but for any number of points. In the set of data, below, it’s visually clear that the red dot is at the center of the blue points.
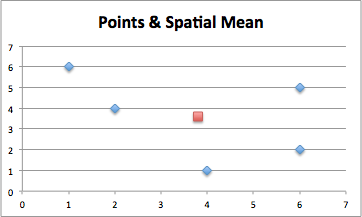
To calculate this mathematically all you have to do is take the average X and Y values of the points, and plot that. See calculation below:
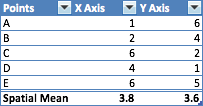
Calculating Geospatial Mean: Applying Spatial Mean to My Bachelor Party
While this is all fine and well conceptually, my friends don’t live in an Excel spreadsheet. I needed to find an easy way to get each friend’s X and Y values. Thankfully, this is exactly what longitude and latitude are for (and you thought you wouldn’t use 3rd grade science)!
Methodology
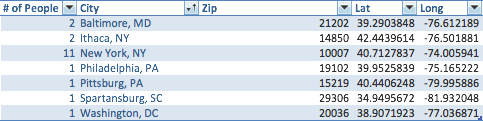
I use the Google Maps API to find the Latitude and Longitude of the city center each of my friends live in (this is an approximation - but I don’t have their exact addresses, so it’ll be close enough). Inputs are below:
Visually:
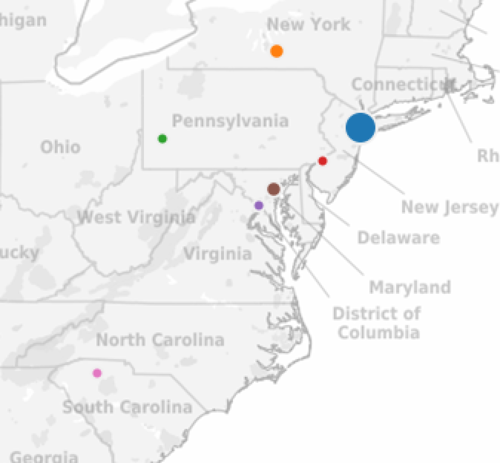
Note: the size of the dot represents how many people from that city.
Calculating Results
Now, to actually calculate the geospatial mean, I need to take the weighted average of these points. In other words, I need to make sure that New York (with 11 of the 19 people attending) is weighted more heavily in determining the location than Spartansburg, SC, which has just one person. Mathematically, I do this by essentially counting the data as if I had 19 points, some of which have the same location.

Calculating spatial mean this way, we see that the spatial mean latitude is 40.295 and longitude -75.50.
Results
As you can see, the Central Point (at Lat = 40.295 and Long = -75.5) is not in the “middle” of all the other locations, but it is in the weighted middle given the large number of people from NYC. This Central Point (which happens to be in Belvidere, New Jersey) is the most fair and central point for all 19 attendees. In other words, it minimizes the average distance for all people traveling to the event.
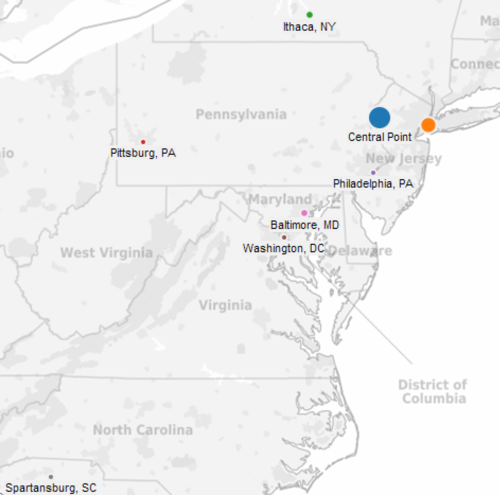
Editors note: I decided to put the bachelor party 17 miles away in the Pocono mountains. Not the exact spatial mean - but very close!
Non-Bachelor Party Uses
The Spatial Mean (specifically the weighted spatial mean) can be used in two main ways in industry:
Supply Chain: This can also be very helpful in terms of deciding where to build supply chain infrastructure. If you run a dropship or DSD business, the spatial mean will help determine the cost-minimizing location (e.g the place where shipping distances will be the lowest, weighted by # of orders).
Storefront Locations: In Retail, Banking, and others store-front heavy industries, spatial mean of a group of customers can help in determining the best location to put a new store. E.g, if you have a group of customers in a certain geographic area, you can take those people’s zip and determine the most central location, weighted by the number of customers (or, perhaps their spend). Caveat’s here include the need to understand how far customers are willing to travel (e.g you can’t just put something in the middle of nowhere, exactly 50 miles away from every major population center.
Summary
Spatial Mean is a good way of finding the true geographic center of a group of people. In this case, this helped my determine a convenient place for my bachelor party (~30 minutes away from the spatial mean suggested location), but the analysis can be easily applied elsewhere.